Minimum Cost Tree From Leaf Values

Problem:

Minimum Cost Tree From Leaf Values

Given an array of n positive integers, the values in the array map to the leaves of a binary search tree from left to right. (A leaf node is defined as node without child.)

The tree has to obey the following rules:

1. Each node has either 0 or 2 children;

2. The value of each non-leaf node is equal to the product of the largest leaf value in its left and right subtree respectively.

Among all such binary trees, find the one with the smallest sum of the values of all non-leaf node, return its non-leaf node sum.

For Example:

Given array [5,2,3]

return 21.

Explain:

With 5, 2, 3 as leaves from left to right, there are two possible node arrangements that fits the 2 rules. 

Tree 1 for example, 10 is the sum of 5x2 (product of max leaf at left and right subtrees), 15 is the product of max leaf in the left tree, whih is 5 and the max leaf in the right tree, which is 3.

Tree 2 for example, 6 is the sum of 2x3 (product of max leaf at left and right subtrees), 15 is the product of max leaf in the left tree, which is 5, and the max leaf in the right tree, which is 3.

The first has non-leaf node sum 15+10=25, and the second has non-leaf node sum 15+6=21. So the answer should be 21.

    15            15

   /  \          /  \

  10   3        5    6

 /  \                 / \

5    2             2   3

Solution:

It looks like a strange problem at the first glance. However, if we consider a real life scenario, it starts to make sense. 

Imagine you are the organizer of a tournament for n players. The price you pay for a match is depends on the 2 players. One reasonable price for a match is price[player1]*price[player2], another price model price[player1] + price[player2] could also be reasonable, how we model it doesn't matter, both price model go to the same direction. Now you want to arrange the matches until we have a champion. The goal is to minimize your cost.

As the organizer, you can do this. You find the weakest player that is still in the game, and will be eliminated in the next match. In order to pay less for that match, you want to choose the weakest opponent possible. With the constraint that "Given an array of n positive integers, the values in the array map to the leaves of a binary search tree from left to right.", you can only choose the opponent next to the weakest player (left or right). So, in order to remove a[i] from the game array a, you need to pick min(a[i-1], a[i+1]), the cost for this match will be a[i] * min(a[i-1], a[i+1]). Keep doing this, we can find the matching arrangement with minimum cost. As a bonus you probably get the highest watching rates because this arrangement favors close matches!

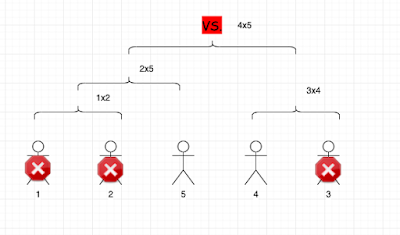min cost games

class Solution {
  public static void main(String...args) {
    System.out.println(minCost(new int[]{5,2,3}));
  }

  private static int minCost(int[] a) {
    int cost = 0;
    int N = a.length;
    while(N > 1) {
      int ko = findMin(a, N);
      cost += a[ko] * minNeighbor(a, ko, N);
      removeElement(a, ko, N);
      N--;
    }
    return cost;
  }

  private static int minNeighbor(int[] a, int ko, int N) {
    if(ko - 1 >= 0 && ko + 1 < N) {
      return Math.min(a[ko-1], a[ko+1]);
    } else {
      if(ko - 1 < 0) return a[ko+1];
      else return a[ko-1];
    }
  }

  private static void removeElement(int[] a, int ko, int N) {
    for(int i = ko; i < N-1; i++) {
      a[i] = a[i+1];
    }
  }

  private static int findMin(int[] a, int N) {
    int min = Integer.MAX_VALUE;
    int index = 0;
    for(int i = 0; i < N; i++) {
      if(min > a[i]) {
        min = a[i];
        index = i;
      }
    }
    return index;
  }
}

Time complexity is O(N^2), because at out loop, we need N matches to eliminate the N-1 players, in the inner loop, need to find the global min in the array and remove it from the array, which cost O(N).

The extra space complexity is O(1), for we reuse the original array to store the players which are still in the game.