XYZ CODE: Binary Tree PreOrder Traversal

Problem

Given a binary tree, return the preorder traversal of its nodes' values.

For Example:

Given:
1
\
2
/ \
3 4

Output: [1,2,3,4]
Follow up: are you able to do it iteratively?

Solution

The preorder recursive traversal took O(N) time cost to visit all the nodes. The caller stack is ~logN on average and N at worst, each stack has finite number of variables. so that gives the space cost O(logN) to O(N).

For iterative solution, we need to store lots of nodes so that we can trace back. This is similar to Inorder traversal. When we traversal to the left most node, we can print the route we reach there, we also store the nodes on a stack so that we can trace back. After we reach the left most node, we use the stack to trace back. After we pop out a node, before pop out another node, we should process the right node. We do the same thing, walk down the subtree until reach left most node, print the path, at the same time store all the nodes in the stack, then we trace back. Each node is push in and pop out of the stack once, the time cost is O(N). The space is bound by the stack size, which is O(N).

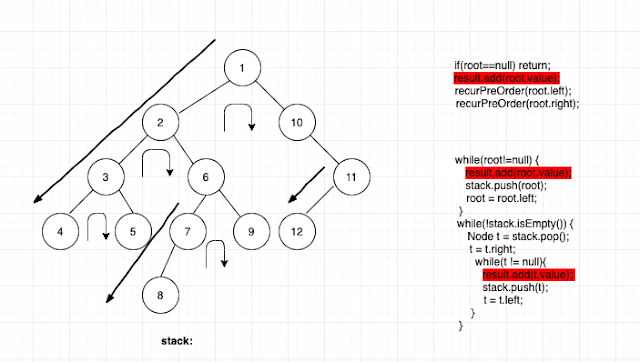BST preorder travesal

import java.util.*;
class PreOrder{
public static void recurPreOrder(Node root, List<Integer> preOrder) {
if(root == null) return;
preOrder.add(root.value);
recurPreOrder(root.left, preOrder);
recurPreOrder(root.right, preOrder);
}
public static void iterPreOrder(Node root, List<Integer> preOrder) {
Stack<Node> stack = new Stack<>();
while(root != null) {
preOrder.add(root.value);
stack.push(root);
root = root.left;
}
while(!stack.isEmpty()) {
Node t = stack.pop();
t = t.right;
while(t != null) {
preOrder.add(t.value);
stack.push(t);
t = t.left;
}
}
}
public static void main(String...args) {
Node root = new Node(6,
new Node(4, new Node(2, null, null), new Node(5, null, null)),
new Node(8, new Node(7, null, null), new Node(9, null, null))
);
List<Integer> preOrder = new ArrayList<>();
recurPreOrder(root, preOrder);
for(int i : preOrder) {
System.out.print(i + " ");
}
System.out.println();
preOrder = new ArrayList<>();
iterPreOrder(root, preOrder);
for(int i : preOrder) {
System.out.print(i + " ");
}
}
private static class Node {
int value;
Node left;
Node right;
public Node(int value, Node left, Node right) {
this.value = value;
this.left = left;
this.right = right;
}
}
}

Time cost O(N), space cost O(N).