detect loop in linked list

back>

Problem:

Detect loop in the linked list.

linked list with loop

A linked list can have loop in it, if a later node's next node points to an earlier node, then we get a loop in the linked list.

We need to clarify the following points:

• does the linked list has header node?
• can the linked list be null?
• what is the value type, int?
• the linked list can have at most one loop, because it is single linked list.

Solution 1, brutal force.

A straight-forward solution will be traversal the linked list, while traversal, the visited nodes are added into a HashSet. The HashSet's contains(currentNode) is called to tell if we visited the same node before. If it was visited, then a loop is detected. If we reached the end of the linked list and not found any node already in the HashSet, then no loop is detected. 

We need to traversal the linked list once, the time complexity of the solution is O(N).

We need a HashSet to store the visited node, a variable to store the current node, the space complexity is O(N).

Solution 2. fast/slow pointer.

We can have 2 pointers both start at the first node. For each iteration, the fast pointer advances 2 steps by calling current = current.next.next, while the slow pointer advances 1 step by calling current = current.next. If there is a loop in the linked list, the fast pointer will travel the loop (more than one time) and meet the slow pointer, otherwise, the fast pointer will travel to the tail of the linked list, which is null.

We need to travel the linked list at least once, the time complexity is O(N).
We need 2 pointer to store the current positions, the space complexity is O(1).

The example code:

LNode.java

loopdetectionsolutiononejava

LoopDetectionSolutionOneTest.java


Sometime we need to find out the entry node of the loop. An extended problem is:

Problem:
Given a linked list, return the first node of its loop if there is one, or return null if there is no loop.

Solution One. 2 pointers.

In the previous problem, when the fast pointer and slow pointer meet, the slow pointer has traveled s steps, while the fast pointer has traveled 2s steps. If the loop's length is r, the fast pointer has traveled nr more steps than the slow pointer, where n >= 1.

2s = nr + s

which is s = nr

Given L as the linked list's length, x as the distance between the loop's entry point and the pointers meet point, y as the distance from the head to the entry point. We will have:

y + x = s = nr

y + x = (n - 1)r + r = (n - 1)r + L - y

y = (n - 1)r + (L - y - x)

Since r = (L - y - x) + x, then (L - y - x) is the distance from the pointers' meet point to the entry point of the loop.

We can set 2 pointers, one starts at the head, the other starts at that meeting point during loop detection. The 2 pointers advance 1 step at a time. When they first meet, one pointer has traveled distance of y, the other pointer has traveled (L - y - x) plus a few loops (n - 1)r. They must meet at the entry point of the loop.

We need to travel the linked list at least once, the time complexity is O(N).
We need 2 pointer to store the current positions, the space complexity is O(1).

Solution 2. Brutal force.

As we did before, using a HashSet to store the nodes visited, the first repeating nodes is the entry point of the loop.

We need to traversal the linked list once, the time complexity of the solution is O(N).

We need a HashSet to store the visited node, a variable to store the current node, the space complexity is O(N).

Example Code:

LoopEntryPointSolutionOne.java
LoopEntryPointSolutionOneTest.java

Detecting loop can also be used in other problems.

Given 2 linked list, we check each one of them for the loop. There are 3 possible scenarios:

1. neither of them has loop.
2. one has loop, the other doesn't have loop.
3. both have loop.

Problem:

Tell if two single linked lists have overlap. 

Analyze: 

First of all, we need to ask if the linked lists can have loop or not. Assuming there is no loop in any of the linked list. The two linked lists are single linked, means if they have overlaps, they share the same nodes from the first overlap node to the last overlap node, which is the common tail. The overlapped linked list should be the Y shape.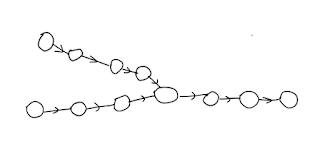 

Y-shaped linked lists

Solution one: brutal force.

We can traversal the first linked list, store its nodes into a HashSet. We then traversal the second linked list, the first node that is contained in the HashSet is where the two linked lists overlaps.

We need to traversal both linked list, the time complexity is O(n1 + n2).
We need to store the first linked list in a HashSet, the space complexity is O(n1).

Solution two: convert to linked list with loop.

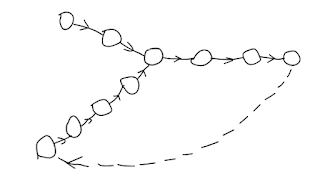attach a tail to a head

Attach the first linked list's tail to the second linked list's head, then use fast/slow pointer to detect loop.

We need to traversal the converted linked list at least once, the time complexity is O(n1 + n2).
We need 2 pointers during the traversal, the space complexity is O(1).

Solution Three: detect common tail.

If the two linked list has common nodes, they must share the same common tail. Traversal the two linked list to the tail, then check if the two tails are the same node.

We need to traversal both linked lists twice, the time complexity is O(n1 + n2).

We only need two pointers to traversal the two linked lists, the space complexity is O(1).

Example Code:

OverlapDetection.java
OverlapDetectionTest.java

Problem:
Find the first overlapping node for two overlapping linked list, return null if there is no overlap.

Solution one: brutal force.

We can traversal the first linked list, store its nodes into a HashSet. We then traversal the second linked list, the first node that is contained in the HashSet is where the two linked lists overlaps.

We need to traversal both linked list, the time complexity is O(n1 + n2).
We need to store the first linked list in a HashSet, the space complexity is O(n1).

Solution two: convert to linked list with loop.

Attach the first linked list's tail to the second linked list's head, then use fast/slow pointer to detect loop. The entry point of the loop is the first overlapping node of the linked lists.

We need to traversal the converted linked list at least once, the time complexity is O(n1 + n2).
We need 2 pointers during the traversal, the space complexity is O(1).

attach a tail to a head

Solution Three: detect common tail.

If the two linked list has common nodes, they must share the same common tail. Traversal the two linked list to the tail, then check if the two tails are the same node.

In order to find the first overlapping node, we can remember the length of the two linked list n1, n2. Then we traversal the linked lists the second time. We can have one pointer travel n1 - n2 steps, then have both pointers advance 1 step at a time. When they first meet, the node is the first overlapping node.

We need to traversal both linked lists twice, the time complexity is O(n1 + n2).

We only need two pointers to traversal the two linked lists, the space complexity is O(1).

FirstOverlapDetection.java

FirstOverlapDetectionTest.java

Problem:
If the linked lists can have loop, tell if they have overlap.

Analyze:

overlap linked lists sharing common loop 1

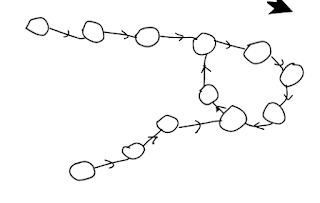overlap linked lists sharing common loop 2

overlap linked lists sharing common loop 3

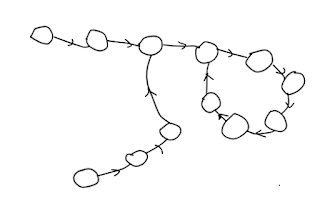The problem can be divided into 2 cases:

1. If one linked list has loop but the other linked list doesn't has loop, they won't overlap.
2. If both lined lists have loops, they must share the common loop if they overlap.

Solution One: Brutal force

traversal the first linked list, store the nodes into a HashSet until meet duplicate node.

traversal the second linked list, store the nodes into a HashSet until meet duplicate node.

Then use HashSet's retainAll method to find the common nodes.

In order to find the first overlapping point, we can traversal the first and second linked list until find the elements in common nodes collection.

We need to traversal both linked list twice, the time complexity is O(n1 + n2).

We need to store both linked list before calling HashSet's retainAll method, the space complexity is O(n1 + n2).

Solution Two: Convert to linked lists without loop

traversal the first linked list, find the entry point of the loop.
traversal the second linked list, find the entry point of the loop. While traversal, check if the first linked list's entry point overlaps with any of the node visited.

In order to find the first overlapping point. We need to divide the problem into two scenarios:

1. the first and second linked lists share the same loop entry point. 
2. the first and second linked lists have different loop entry points.

For scenario 1, we set the common entry point's next node to null, in order to break the common loop. Then the problem become finding the first overlap node for two linked lists without loop.

For scenario 2, the first overlapping node for the two linked lists are their loop entry nodes.

We need to traversal each linked list twice, the time complexity is O(n1 + n2).

We only need a few pointers during the traversal, the space complexity is O(1).

FirstOverlapDetectionGeneral.java

FirstOverlapDetectionGeneralTest.java

Take Away:

From the above solutions, we learned a very important technique -- using multiple pointers to traversal the linked list.

Problem:

Detect the last K nodes of a linked list.

This is a very simple problem now, no more discussion needed here (is it?).